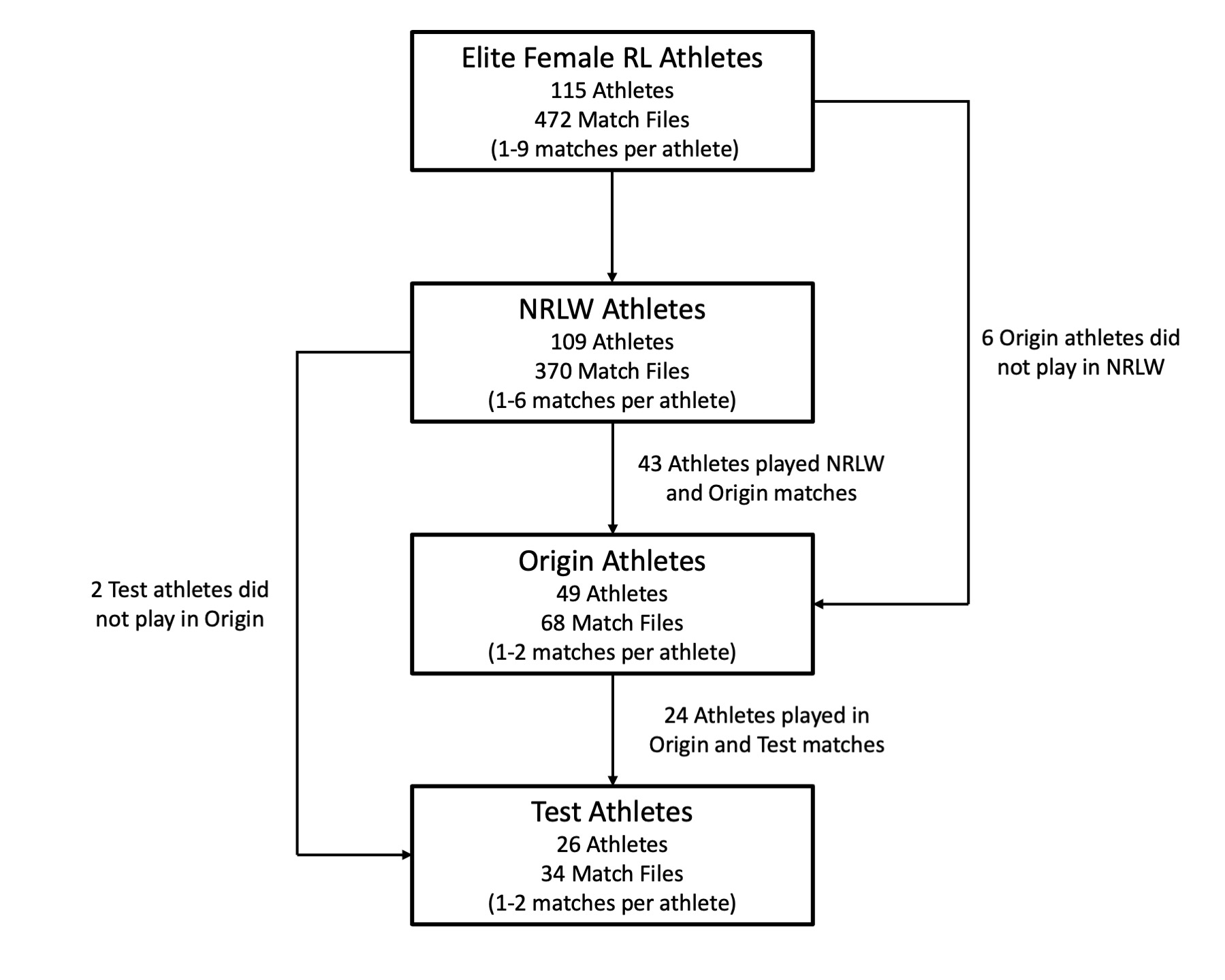
Andersson, H., Randers, M., Heiner-Møller, A., Krustrup, P., & Mohr, M. (2010). Elite female soccer players perform more high-intensity running when playing in international games compared with domestic league games.
The Journal of Strength and Conditioning Research,
24(4), 912–919.
https://doi.org/10.1519/jsc.0b013e3181d09f21
Bartlett, J., Hatfield, M., Parker, B., Roberts, L., Minahan, C., Morton, J., & Thornton, H. (2020). DXA-derived estimates of energy balance and its relationship with changes in body composition across a season in team sport athletes.
European Journal of Sport Science,
20(7), 859–867.
https://doi.org/10.1080/17461391.2019.1669718
Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting linear mixed-effects models using lme4.
Journal of Statistical Software,
67(1), 1–48.
https://doi.org/10.18637/jss.v067.i01
Bellinger, P., Ferguson, C., Newans, T., & Minahan, C. (2020). No influence of prematch subjective wellness ratings on external load during elite
Australian Football match play.
International Journal of Sports Physiology and Performance,
15(6), 801–807.
https://doi.org/10.1123/ijspp.2019-0395
Borg, D., Nguyen, R., & Tierney, N. (2021). Missing data: Current practice in football research and recommendations for improvement.
Science and Medicine in Football,
0(ja), null.
https://doi.org/10.1080/24733938.2021.1922739
Dalton-Barron, N., Whitehead, S., Roe, G., Cummins, C., Beggs, C., & Jones, B. (2020). Time to embrace the complexity when analysing GPS data? A systematic review of contextual factors on match running in rugby league.
Journal of Sports Sciences,
38(10), 1161–1180.
https://doi.org/10.1080/02640414.2020.1745446
Ferris, D., Gabbett, T., McLellan, C., & Minahan, C. (2018). Basal markers of inflammation, muscle damage, and performance during five weeks of pre-season training in elite youth rugby league players.
Journal of Athletic Enhancement,
7(2).
https://doi.org/10.4172/2324-9080.1000286
Gallo, T., Cormack, S., Gabbett, T., & Lorenzen, C. (2017). Self-reported wellness profiles of professional
Australian Football players during the competition phase of the season.
The Journal of Strength and Conditioning Research,
31(2), 495–502.
https://doi.org/10.1519/jsc.0000000000001515
Govus, A., Coutts, A., Duffield, R., Murray, A., & Fullagar, H. (2018). Relationship between pretraining subjective wellness measures, player load, and rating-of-perceived-exertion training load in american college football.
International Journal of Sports Physiology and Performance,
13(1), 95–101.
https://doi.org/10.1123/ijspp.2016-0714
Griffin, J., Larsen, B., Horan, S., Keogh, J., Dodd, K., Andreatta, M., & Minahan, C. (2020). Women’s football: An examination of factors that influence movement patterns.
The Journal of Strength & Conditioning Research,
34(8), 2384–2393.
https://doi.org/10.1519/jsc.0000000000003638
Griffin, J., Newans, T., Horan, S., Keogh, J., Andreatta, M., & Minahan, C. (2021). Acceleration and high-speed running profiles of women’s international and domestic football matches.
Frontiers in Sports and Active Living,
3, 71.
https://doi.org/10.3389/fspor.2021.604605
Halson, S. (2014). Monitoring training load to understand fatigue in athletes.
Sports Medicine,
44(2), 139–147.
https://doi.org/10.1007/s40279-014-0253-z
Hannon, M., Coleman, N., Parker, L. J., McKeown, J., Unnithan, V., Close, G., Drust, B., & Morton, J. (2021). Seasonal training and match load and micro-cycle periodization in male premier league academy soccer players.
Journal of Sports Sciences,
39(16), 1838–1849.
https://doi.org/10.1080/02640414.2021.1899610
Haugnes, P., Torvik, P.-Ø., Ettema, G., Kocbach, J., & Sandbakk, Ø. (2019). The effect of maximal speed ability, pacing strategy, and technique on the finish sprint of a sprint cross-country skiing competition.
International Journal of Sports Physiology and Performance,
14(6), 788–795.
https://doi.org/10.1123/ijspp.2018-0507
Hopkins, W., Marshall, S., Batterham, A., & Hanin, J. (2009). Progressive statistics for studies in sports medicine and exercise science.
Medicine & Science in Sports & Exercise,
41(1), 3–12.
https://doi.org/10.1249/MSS.0b013e31818cb278
Kenny, D., & Judd, C. (1986). Consequences of violating the independence assumption in analysis of variance.
Psychological Bulletin,
99(3), 422–431.
https://doi.org/10.1037/0033-2909.99.3.422
Lenth, R. (2020).
Emmeans: Estimated marginal means, aka least-squares means.
https://CRAN.R-project.org/package=emmeans
Lüdecke, D. (2020).
sjPlot: Data visualization for statistics in social science.
https://CRAN.R-project.org/package=sjPlot
Lüdecke, D., Ben-Shachar, M., Patil, I., Waggoner, P., & Makowski, D. (2021). Performance: An r package for assessment, comparison and testing of statistical models.
Journal of Open Source Software,
6(60), 3139.
https://doi.org/10.21105/joss.03139
Lüdecke, D., Patil, I., Ben-Shachar, M., Wiernik, B., Waggoner, P., & Makowski, D. (2021). See: An r package for visualizing statistical models.
Journal of Open Source Software,
6(64), 3393.
https://doi.org/10.21105/joss.03393
McCaskie, C., Young, W., Fahrner, B., & Sim, M. (2019). Association between preseason training and performance in elite
Australian football.
International Journal of Sports Physiology and Performance,
14(1), 68–75.
https://doi.org/10.1123/ijspp.2018-0086
McElreath, R. (2018).
Statistical rethinking: A bayesian course with examples in r and stan. Chapman; Hall/CRC.
https://doi.org/10.1201/9781315372495
Nakai, M., & Ke, W. (2011). Review of the methods for handling missing data in longitudinal data analysis. International Journal of Mathematical Analysis, 13.
Newans, T., Bellinger, P., Buxton, S., Quinn, K., & Minahan, C. (2021). Movement patterns and match statistics in the national rugby league women’s (NRLW) premiership.
Frontiers in Sports and Active Living,
3.
https://doi.org/10.3389/fspor.2021.618913
Quinn, K., Newans, T., Buxton, S., Thomson, T., Tyler, R., & Minahan, C. (2020). Movement patterns of players in the Australian Women
’s Rugby League team during international competition.
Journal of Science and Medicine in Sport,
23(3), 315–319.
https://doi.org/10.1016/j.jsams.2019.10.009
R Core Team. (2019).
R: A language and environment for statistical computing. R Foundation for Statistical Computing.
https://www.R-project.org/
Rago, V., Krustrup, P., Martín-Acero, R., Rebelo, A., & Mohr, M. (2020). Training load and submaximal heart rate testing throughout a competitive period in a top-level male football team.
Journal of Sports Sciences,
38(11-12), 1408–1415.
https://doi.org/10.1080/02640414.2019.1618534
Thornton, H., Armstrong, C., Rigby, A., Minahan, C., Johnston, R., & Duthie, G. (2020). Preparing for an
Australian Football League Women’s League season.
Frontiers in Sports and Active Living,
2, 216.
https://doi.org/10.3389/fspor.2020.608939
Thornton, H., Nelson, A., Delaney, J., Serpiello, F., & Duthie, G. (2019). Interunit reliability and effect of data-processing methods of global positioning systems.
International Journal of Sports Physiology and Performance,
14(4), 432–438.
https://doi.org/10.1123/ijspp.2018-0273
Tierney, P., Blake, C., & Delahunt, E. (2021). Physical characteristics of different professional rugby union competition levels.
Journal of Science and Medicine in Sport,
24(12), 1267–1271.
https://doi.org/10.1016/j.jsams.2021.05.009
Yarkoni, T. (2019). The generalizability crisis.
Behavioral and Brain Sciences, 1–37.
https://doi.org/10.1017/S0140525X20001685